Zestaw kontrolny nr 3
![]()
Niech a[n] oznacza liczbę słów długości n nad alfabetem {0,1,2}, które nie zawierają podsłowa 00.
Znajdź wzór rekurencyjny dla ciągu a[n].
Jeśli n=1, to istnieją 3 słowa spełniające warunki zadania: {0},{1} oraz {2}, zatem a[1]=3.
Jeśli n=2, to do dyspozycji mamy następujące słowa: {0, 1}, {0, 2}, {1, 0}, {1, 1}, {1, 2}, {2, 0}, {2, 1}, {2, 2} i stąd a[2]=8.
Dla n=3 słowa, które spełniają warunki zadania to: {0, 1, 0}, {0, 1, 1}, {0, 1, 2}, {0, 2, 0}, {0, 2, 1}, {0, 2, 2}, {1, 0, 1}, {1, 0, 2}, {1, 1, 0}, {1, 1, 1}, {1, 1, 2}, {1, 2, 0}, {1, 2, 1}, {1, 2, 2}, {2, 0, 1}, {2, 0, 2}, {2, 1, 0}, {2, 1, 1}, {2, 1, 2}, {2, 2, 0}, {2, 2, 1}, {2, 2, 2} - jest ich 22 i stąd a[3]=22.
Załóżmy, że mamy słowo spełniające warunki zadania o długości n.
Jeśli ostatnią cyfrą tego słowa jest 1, czyli a[n] jest postaci {..........,1}, to takich słów jest a[n-1].
Jeśli ostatnią cyfrą tego słowa jest 2, czyli a[n] jest postaci {..........,2}, to takich słów jest a[n-1].
Jeśli ostatnią cyfrą tego słowa jest 0, to na przedostaniej pozycji musi być 1 lub 2, czyli: {.........,1,0} bądź {.........,2,0}. W każdym z tych przypadków mamy a[n-2] słów.
W sumie daje nam to a[n-1]+a[n-1]+a[n-2]+a[n-2] prawidłowych słów o długości n, czyli zależność rekurencyjna jest postaci : a[n]=2 a[n-1]+2 a[n-2].
Dla n=0 wynikiem jest puste słowo, które oczywiście spełnia warunki zadania i stąd możemy przyjąć a[0]=1.
Ostatecznie rekurencja ma postać: ![]()
Korzystając z dobrodziejstw programu Mathematica postanowiłem sprawdzić powyższe rozumowanie.
Zdefiniuję rekurencję wg powyższego wzoru:

Oto kilka wyrazów:
![]()
![]()
![]()
![]()
![]()
![]()
W Mathematica wszystkie słowa o długości n nad alfabetem wypisze funkcja:
![]()
Na przykład:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
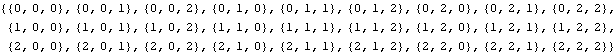
Bazując na tej funkcji tworzę inną, która zwraca liczbę takich słów, w których dwa zera nie występują obok siebie:
![]()
Length[f[n]] - zwraca liczbę słów o długości n nad alfabetem {0,1,2};
Count[f[n],{___,0,0,___} - zwraca liczbę słów, w których występują dwa zera obok siebie;
Oba ciągi: a[n] oraz b[n] powinny zwracać te same wartości - sprawdźmy:
![]()
| 0 | 1 | 1 |
| 1 | 3 | 3 |
| 2 | 8 | 8 |
| 3 | 22 | 22 |
| 4 | 60 | 60 |
| 5 | 164 | 164 |
| 6 | 448 | 448 |
| 7 | 1224 | 1224 |
| 8 | 3344 | 3344 |
| 9 | 9136 | 9136 |
| 10 | 24960 | 24960 |
![]()
Znajdź wzór zwarty ciągu określonego wzorem rekurencyjnym:
![]()
Ponieważ podana rekurencja jest liniowa zatem postępujemy następująco:
Przesuwamy indeksy przez podstawienie n->n+2, co daje:
![]()
Tworzymy równanie rozwiązujące przez podstawienie ![]() otrzymując :
otrzymując :
![]()
Dzieląc obustronnie przez λ otrzymujemy równanie kwadratowe:
![]() ,
,
którego ma dwa różne rozwiązania rzeczywiste:
![]()
Stąd ciąg ![]() jest kombinacją liniową ciągów geometrycznych o ilorazach
jest kombinacją liniową ciągów geometrycznych o ilorazach ![]() :
:
![]()
Współczynniki α i β znajdziemy z warunków początkowych rekurencji:
![]()
Rozwiązaniem jest:
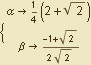
Łącząc rozwiązania ![]() z wyznaczonymi wartościami współczynników α i β otrzymujemy postać zwartą wzoru:
z wyznaczonymi wartościami współczynników α i β otrzymujemy postać zwartą wzoru:
![]()